[CF1586I] Omkar and Mosaic 题解

下文中：

• 视题目中的两种颜色为黑色与白色。图示中所有颜色均只是为了表示颜色的相同或不同，且白色代表未填充。
• 记 表示第 行第 列的格子。
• 认为两个格子“相等”或“不等”，当且仅当两个格子的颜色相同或不同。

---

难点在于观察性质。

考虑在没有任何限制的情况下，一组合法解有哪些性质。有两个基本性质是：

• 位于角落的格子的颜色与其相邻的格子颜色相同。
• 对于一个不在边缘的格子，它的四联通中，恰好有 个黑色格子与 个白色格子。

---

初始我们没有进行任何涂色。

---

根据第一个性质，可以如下涂色。

---

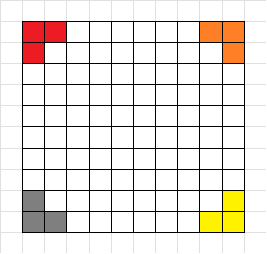
根据第二个性质，可以不断扩展。

---

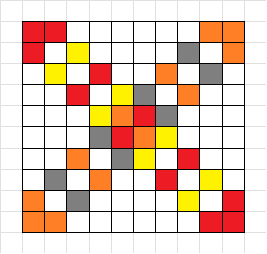
注意到，当 为奇数时，中间格子的颜色一定会产生冲突，所以 为奇数时一定不合法。

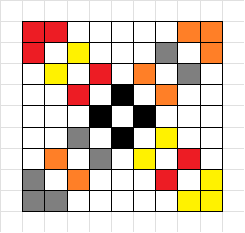
为什么

对于主对角线，有 ；对于副对角线，有 。

---

依然是由于第二个性质，对于如图所示的这些斜列，每个斜列的颜色都是黑白交替的。图中只展示了一个方向的斜列，另一个方向同理。

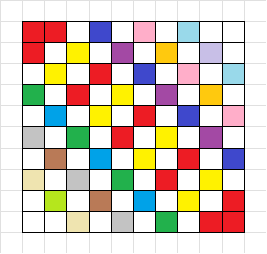
为什么

例如对于 ，第二个性质要求 中两黑两白，又因为 ，所以 。

其余位置同理。

---

考虑网格的一个角落，有 ，又有 ，故有 。依此类推，我们可以得到两个重要结论：

• 网格关于主对角线与副对角线对称。
• 有 。

为什么

因为 ，为了让 有两个相邻的格子与它颜色相同，我们只能让 与它颜色相同。

同理。

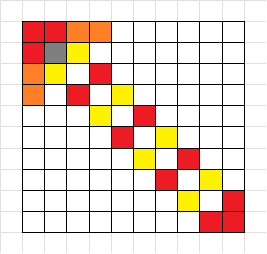
如何“依此类推”

上图的下一步会变成：

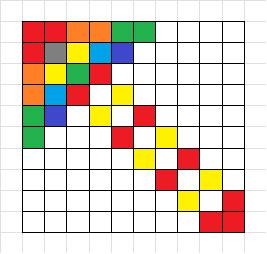
在上图中，颜色是这样确定的：

• ：因为 ，所以 ，也就是（部分）斜列颜色黑白交替的性质。
• ：与 同理，且显然有 。
• ：与 同理，因为 ，所以 。
• ：与 同理，且显然有 。

下一步会变成：

最后会变成：

最后这图只能当成乐子看。

---

可以证明，上述条件是充要的。

考虑题目中给的限制。我们可以根据斜列与对称的关系，将所有限制都转化到第一行，再根据 尝试补全第一行。最后，若第一行被补全了，那么有唯一解；若第一行未被补全，那么有多解；若转化与补全过程中有矛盾，那么无解。

若有唯一解，再根据第一行推出整个网格即可。

代码是好写的，就不放了（实则是因为我的代码写得一坨）。